-
미분, 시그마, 시그모이드 함수cs231n 강의 2022. 4. 30. 00:31
▶ 초심공룡을 아는가, 그 모임엔 막내가 정말 치명적이다.
cs231n 강의에 미분과 시그마를 통한 연산이 자주 나온다.
시그모이드란 함수도 역시 알아야 되서 정리한다.
1. 미분
- 순간변화율(또는 미분계수 라고도 함)을 구하는 것이다
- 변화율은 함수를 통해 표현한다
- 변화율을 기울기 라고 얘기한다
- 변화율은 항상 기준이 있어야 구할 수 있다
- 순간 변화율에서 기준은 순간이다
- 여기서 순간은 '한 점' 이다
- 따라서 한 점의 기울기 (순간변화율) 를 구하는 것이다
- 사실 기울기를 구하기 위해선 두 점이 필요하다
- 그런데 미분할때 두 점 사이의 거리는 무한소이기 때문에 그냥 '0' 으로 본다
- 무한소 개념 -> https://ko.wikipedia.org/wiki/%EB%AC%B4%ED%95%9C%EC%86%8C
- 거리가 0 이면 그냥 한 점이나 마찬가지 이므로 한 점을 기준으로 해서 한 점의 기울기(순간변화율) 를 구한다
- '미분 한다 = 도함수를 구한다' 이렇게 볼 수도 있다
- 따라서 순간변화율 = 한 점의 기울기 = 미분계수 = 도함수= 접선의 기울기 이렇게 보면 된다
- 그래프
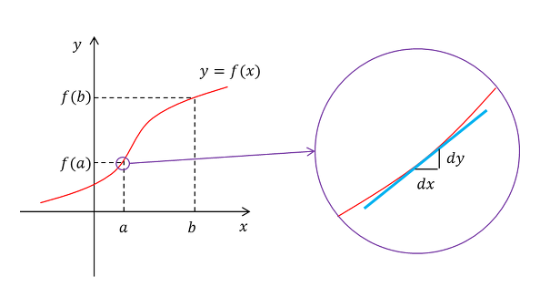
그래프에 빨간 곡선이 있다
( a , f(a) ) 라는 한 점 (순간)을 기준으로 잡고
그림과 같이 확대하면
x = a 일때의 기울기 (변화율) 을 확인할 수 있다
확대한 걸 보면 두 점을 기준으로 기울기를 구했지만 두 점의 거리가 무한소 이므로
두 점의 거리를 0 으로 보기 때문에 한 점으로 본다
- 공식

기본 공식이다
- 참고 링크 https://darkpgmr.tistory.com/45
2. 시그마
- 우리에게 필요한 시그마는 이놈이다

어디선가 한번씩 보았을 것이다
- 순차적으로 정해진 값들을 연산하고 모두 더하라는 뜻이다
- 값을 계속해서 더해나갈 기준이 되는 시작값이 필요하다
- 마지막으로 더할 마지막값이 필요하다
- 이 값들을 대입할 식도 필요하다
- 그림

∑ 의
아래는 시작값을
위는 마지막 값을
오른쪽에는 연산식을 나타낸다
- 예시

n을 1 ~ 5까지 우측의 (n/2)+1 방정식에 대입
대입한 결과값은 3/2 , 2 , 5/2 , 3 , 7/2
위 값들을 모두 더하면 25/2
정답은 25/2 or 12.5
3. 시그모이드 함수
- S자형 곡선 또는 시그모이드 곡선을 갖는 수학 함수이다
- 딥러닝에서 많이 쓰이는 활성화 함수 중 하나이다
- 여러 종류가 있지만 로지스틱 함수 를 알면 된다
- 로지스틱 함수 그래프

그래프를 보면 알 수 있다
독립변수 (x값) 의 값이 무엇이든
종속변수 (y값) 의 값은 0~1 이다
어떤 데이터를 넣어도 0 ~ 1 사이의 결과값을 만든다
때문에 주로 데이터를 카테고리(범주)별로 분류할때 사용한다
- 예시
- 내일 비가 오냐, 안오냐
- 성별 (남자냐 여자냐)
- 대한민국이 월드컵 16강에 진출하냐 못하냐
- 로지스틱 함수 식

'cs231n 강의' 카테고리의 다른 글
cs231n 6강 정리 (0) 2022.05.14 cs231n 5강 정리 (0) 2022.05.04 cs231n 4강 정리 (0) 2022.04.23 Learning rate(Step size), Back propagation, Activation function딥러닝 네트워크 구조, Weight, Bias (0) 2022.04.23 cs231n 3강 정리 (0) 2022.04.16